Which Cross-Validation Method to Use in Machine Learning?
One of the most important decision for your machine learning experiments!
Hi everyone! 👋
How’s your summer going?
It’s been quite a long time since I haven’t published in this newsletter, but recently I’ve been receiving lots of DMs from machine learning practitioners.
I feel it will be much more useful for everyone if I summarize my practical tips in here.
One of the questions I recently received was about selecting the proper cross-validation scheme in a machine-learning experiment.
For those that don’t know, cross-validation is defined as:
Cross-validation is a model validation technique for assessing how the results of a statistical analysis will generalize to an independent data set.
It is used during the training of a machine learning model to figure out how the model will behave once deployed in real life (aka how it will generalize).
The two main issues I’m seeing with practitioners getting bogged down with cross-validation are:
They don’t do cross-validation at all.
They do not choose the right cross-validation scheme that fits their use case.
This is problematic because it leads to the dreaded overfitting issue where the model seems to be doing fine during training, but completely collapses in production.
In this issue, I’ll show you a trick to always select the right cross-validation scheme for your use-case!
btw: there is a video version over here if you are more of a visual learner.
What’s the trick?
There are a lot of cross-validation options to choose from:
Luckily for us, it’s fairly straightforward to figure out which fits best a use case.
The trick is as follows:
Think about how your model will be used and interact with data in a deployed setting. Then recreate this environment for the validation of the model.
It’s as simple as that.
There are usually three components interacting together when a model is in production:
There is a data source that generates the input for the model.
There is the trained model per se.
There is the output of the model which should be solving a task.
To get satisfactory output during the production phase, the training of the model and the way the input data is generated need to fit together.
Let’s check an example to illustrate:
Assuming we want to detect the presence of a disease in samples from an unseen patient. How would the model interact with the data in production?
The important part of the interaction above is that the model never saw the patient during its training.
This piece of information is crucially important because it means that during the training of the model, we cannot have data from a single patient in both the training and validation split.
This effectively pinpoints exactly which of the different kinds of cross-validation techniques in the tree of possible schemes to use we should be using.
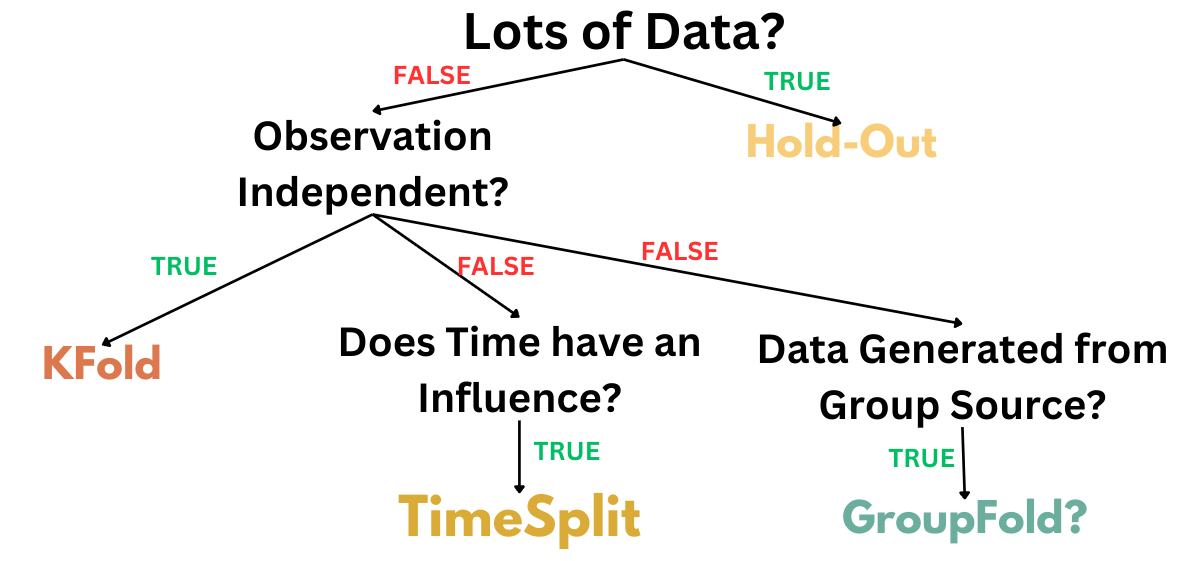
Let’s look at that tree!
Decision Tree of Cross-Validation Techniques
At a glance, the selection process looks like this:
We’ll walk through each of the branches in a minute, but one thing to note is that each of the leaf nodes contains variants that you can use to ensure the cross-validation score match the generalization.
Lots of Data? - True
If you have a lot of data, your cross-validation usually is very simple.
It will consist most of the time of doing a simple hold-out cross-validation, where about 80% of your data is used for training and 20% is used for testing.
The reason for that is that both the training and test sets are so large that they are equally representative of the data in general.
Let’s use our production trick to illustrate this:
If you were training a large language model to do autocomplete based on user generated prompt, the setup would look like this:
The data generator is an independent human that wrote a bit of text with a missing word. The model is GPT and the output is the same prompt, but with the most likely word added at the end.
In that particular scenario, if you train with enough data like common crawl billions of internet pages or Reddit discussions, you get enough data generators (i.e. independent humans) to have a similar distribution however you cut the data during testing.
Therefore, when your model is faced with the showcased input in production, it isn’t that much different from how it was trained.
Disclaimer: This might not hold all the time, for instance when you have very very strong dependency between data points or when the distribution is completely skewed during testing (i.e. someone prompt in a language the model never saw before).
But in most cases it generally does.
Lots of Data? - False
Now, when you don’t have lots of data it means that you have to be very careful in how you do the cutting and validation during training.
The first question to ask yourself is if your observations are independent of each other or not.
Assuming that some data is Independent and Identically Distributed (i.i.d.) is making the assumption that all samples stem from the same generative process and that the generative process is assumed to have no memory of past generated samples.
This assumption is common in machine learning but it very rarely holds 100%. What you want to check here is if the independent and identically distributed assumption kinda hold.
Observation Independent? - True
So let’s say it does hold.
Here it means that whatever is generating the data is generating each of them independently without a strong correlation between data points.
Let’s consider the following example:
Given a newly created product on a store, predict whether its first review will be positive or negative.
In this case, the data generator is the user base which are creating a single review for a new product. The new product meta information is the input to the system. The model was trained with these reviews in some ways and the label is binary.
In that particular case, if we assume that no one group of users is dominating the review process for the first review of a new product, we can say it’s IID.
This would have been perfect for a hold-out split if we had Amazon level of data, but if we don’t we need to use Kfold to generate a proper estimate of the model generalization performance.
KFold is super simple.
Chunk your data into equally sized blocks, train on one bunch of blocks, and test on the other. Then you alternate which block is the testing block and which ones are the training blocks.
Usually, 5 to 10 folds are good enough to have a good estimate of the performance of the model.
There are other variation of KFold like stratified and shufflesplit, depending if your classes are severely imbalanced or if you don’t have much data.
Observation Independent? - False
But, let's say that the IID assumption doesn’t hold at all.
The first thing to figure out is if the observations have time dependencies.
Observation Time Dependent? - True
Time-dependent data points are fairly straightforward.
You can think of them as being generated by a process that over time will generate points sequentially and with full knowledge of the previous data points.
A good example of time-dependent data generation is with stock prices.
One of the most important pieces of information for stock prices is knowledge about historical stock performance.
So in production, if you have the following task:
Given previous information about the stock market, predict the next stock price of a given stock.
You have to take into consideration the time aspect whenever cross-validating. Namely, you cannot train on future stock prices (i.e. t = 3,4,5) and past stock prices (t = 0, 1) to predict a stock price (t = 2).
This will not be possible in production to see the future, therefore when cross-validating you need to “take a walk through your data”.
Which is what a TimeSeriesSplit does.
The first fold will have the least data to train on and you will progressively gather more training data. You will always test on “future” data in this particular case.
Observation Group Dependent? - True
Now, your data points might not be dependent on the time domain.
Maybe it’s something else that make them correlated, like in our earlier example with disease diagnosis.
Consider the following situation:
Given labelled EEG data about patients' emotional states predict what an unseen patient's emotional state will be.
If you didn’t take enough time to explore your data, you might not realize that the data generators (i.e. the brain of the participant) are creating very correlated data points.
The process kind of looks like the above.
If you were to run a clustering algorithm on the data point, you will usually have a very easy time to find back which data points belong to which participant.
Therefore, if we use our production trick we will have something like this:
The data generator is a new participant brain that is generating EEG signals. The model was trained on previous participants and had never seen this participant before. The output labels are the emotional states of this new participant across time.
The perfect methodology for this is GroupFold
It’s the same idea as KFold except that the groups always stay together in either the training or the testing set. In our example, a group is a participant generating multiple data points. Meaning that during testing you can be 100% sure the model never saw that group before.
Conclusion
All in all, don’t forget the simple trick to think hard about how your model will be used in production. Because at the end of the day, it’s kind of the only thing that matters.
If you want to explore the subject a bit more I highly recommend the following resources:
A Gentle Introduction to K-fold Cross-Validation (Machine Learning Mastery)
3.1. Cross-validation: evaluating estimator performance (sklearn docs)
I hope this was useful, if you have any questions don’t hesitate to shoot me a DM.
Have a great rest of the week everyone! 🌹
Best,
Yacine Mahdid